下列不等式成立的有（ ）。

A.x＋2＞5

B.x－1＜2

C.x＞－3

D.2x－1＞5

说明下列表述都可作为a是{a_n}极限的定义:

(2)对任给的ε＞0,存在N∈N₊,当n＞N时,不等式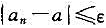成立;

(3)对任给的ε＞0,存在N∈N₊,当n＞N时,不等式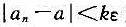成立，其中k是正常数;

(4)对于任给的m∈N₊,存在N∈N₊，当n＞N时，不等式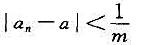成立;

(5)对于任给的ε＞0,存在N∈N₊,使不等式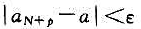对于任意的正整数p都成立。

将如下问题表示为混合整数线性规划模型：

max z=3x₁+f(x₂)+4x₃+g(x₄),

其中

要求满足下列约束条件：

(1)2x₁-x₂+x₃+3x₄≤15;

(2)下面两个不等式至少有一个成立：

x₁+x₂+x₃+x₄≤10，

3x₁-x₂-x₃+x₄≤20；

(3)下列不等式至少有两个成立：

5x₁+3x₂+3x₃-x₄≤30，

2x₁+5x₂-x₃+3x₄≤30,

-x₁+3x₂+5x₃+3x₄≤30，

3x₁-x₂+3x₃+5x₄≤30；

(4)x₃=2或3或4；

(5)x_j≥0(j=1，2，3，4).

A.1个

B.2个

C.3个

D.4个

(1)对于无穷多个ε＞0,存在N∈Z⁺,当n＞N时,使得不等式lχ_n-al＜ε成立;

(2)对于任给的ε＞0,任给N∈Z⁺,存在n＞N,使得不等式lχ_n-al＜ε成立;

(3)对于任给的ε＞0,存在N∈Z⁺,当n≥N时,使得不等式lχ_n-al＜ε成立;

(4)对于任给的ε＞0,存在N∈Z⁺,当n＞N时,使得不等式lχ_n-al＜ε,K∈R⁺成立;

(5)对于任给的m∈Z+,存在N∈Z⁺,当n＞N时,使得不等式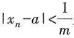成立.

A.－2，－1，0

B.0，1

C.－1，0

D.不存在

下列关于数列的极限是的定义，哪些是对的，哪些是错的？如果是对的，试说明理由；如果是错的，试给出一个反例. (1) 对于任意给定的存在当时，不等式成立； (2) 对于任意给定的存在当时，有无穷多项, 使不等式成立； (3) 对于任意给定的存在当时，不等式成立，其中为某个正常数； (4) 对于任意给定的存在当时，不等式成立.

下列说法能否作为a是数列{an}的极限的定义，为什么？

(1)对于无穷多个ε＞0，存在N∈N⁺，当n＞N时，不等式|a_n-a|＜ε成立;

(2)对于任给ε＞0，存在N∈N⁺，当n＞N时，有无穷多项a_n，使不等式|a_n-a|＜ε成立;

(3)对于任给ε₀=10^-10，不等式|a_n-a|＜10^-10恒成立。

下列说法能否作为a是数列{a_n}的极限的定义？为什么？

(1)对于无穷多个存在N∈N₊,当n＞N时,不等式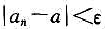成立;

(2)对于任给的存在N∈N₊,当n≥N时,有无穷多项an,使不等式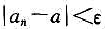成立;

(3)对于给定的很小的正数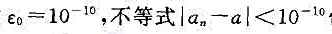恒成立。

将下述问题表示为混合整数规划模型：

min x₀=f₁(x₁)+f₂(x₂)．

其中

且满足下列约束条件：

(1)或者x₁≥10，或者x₂≥10；

(2)下列不等式至少有一个成立：

2x₁+x₂≥15,x₁+x₂≥15,x₁+2x₂≥15;

(3)|x₁-x₂|=0或5或10；

(4)x₁≥0，x₂≥0．

(1)对于任意给定的ε＞0，存在N∈N.，当n＞N时，不等式xn-a＜ε成立;

(2)对于任意给定的ε＞0，存在N∈N.，当n＞N时，有无穷多项x_n，使不等式lx_n-al＜ε成立;

(3)对于任意给定的ε＞0，存在N∈N.，当n＞N时，不等式|x_n-a|＜cε成立，其中c为某个正常数;

(4)对于任意给定的m∈N.，存在N∈N+.当n＞N时，不等式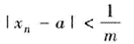成立.