 重要提示:
请勿将账号共享给其他人使用,违者账号将被封禁!
重要提示:
请勿将账号共享给其他人使用,违者账号将被封禁!
 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
 更多“Какая профессия считается престижной сейчас?”相关的问题
更多“Какая профессия считается престижной сейчас?”相关的问题
第1题
| 设f(x)是定义在[-1,1]上的奇函数,且其图象上任意两点连线的斜率均小于零. (1)证明f(x)在[-1,1]上是减函数; (2)如果f(x-c),f(x-c2)的定义域的交集为空集,求实数c的取值范围; (3)证明:若-1≤c≤2,则f(x-c),f(x-c2)存在公共的定义域,并求出这个公共的定义域. |
第2题
| (本小题满分12分) 已知函数 (1) 若 (2) 若 求证: |
第3题
(本题满分15分)已知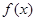 在定义域上是奇函数,且在 在定义域上是奇函数,且在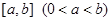 上是减函数,图像如图所示. 上是减函数,图像如图所示.(1)化简: (2)画出函数 (3)证明: |
第4题
(本小题满分16分)已知函数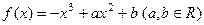 . .(I)当 (II) 若函数 (III)对任意 |
第5题
| 已知函数f(x)=-x3+ax2+b(a,b∈R). (1)若函数y=f(x)的图象上任意不同的两点的连线的斜率小于1,求证:- (2)若x∈[0,1],则函数y=f(x)的图象上的任意一点的切线的斜率为k,求证:1≤a≤ |
第6题
已知函数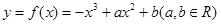 (1)若函数 (2)设函数 (3)若函数 |
第7题
已知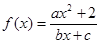 是奇函数,且其图象经过点(1,3)和(2,3)。 是奇函数,且其图象经过点(1,3)和(2,3)。(1)求 (2)用单调性的定义证明: (3) |

 警告:系统检测到您的账号存在安全风险
警告:系统检测到您的账号存在安全风险
为了保护您的账号安全,请在“上学吧”公众号进行验证,点击“官网服务”-“账号验证”后输入验证码“”完成验证,验证成功后方可继续查看答案!
